
What would more realistic graphs look like? How inaccurate is it to ignore the non-constant portion of the motion? What is wrong with this graph? Ask students whether the velocity could actually be constant from rest or shift to negative so quickly. Ask-Can a velocity graph be used to find the position? Can a velocity graph be used to find anything else? Have students describe the relationship between the velocity and the position on these graphs. Then draw a few velocity graphs and see if they can get the corresponding position graph. Students should then be able to see that the corresponding velocity graph is a horizontal line at 0.5km/minute and then a horizontal line at –0.5 km/minute. Ask the students what the velocity is at different times on that graph. Return to the scenario of the drive to and from school.
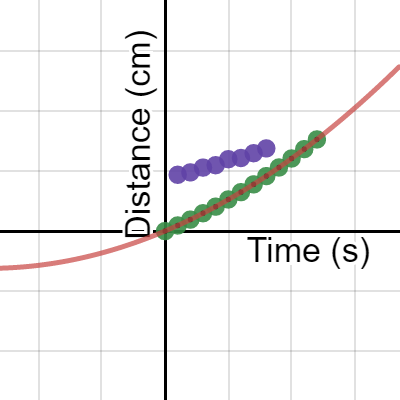
At the beginning of the motion, as the car is speeding up, we saw that its position is a curve, as shown in Figure 2.17. īut what if the velocity is not constant? Let’s look back at our jet-car example.
And in this graph, the y-intercept is v 0.
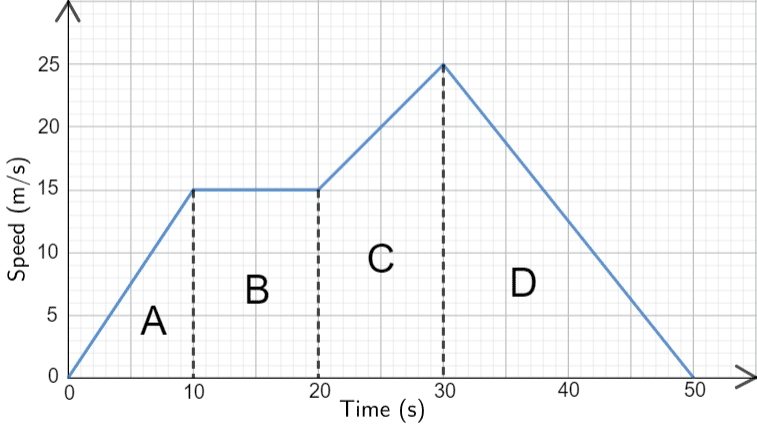
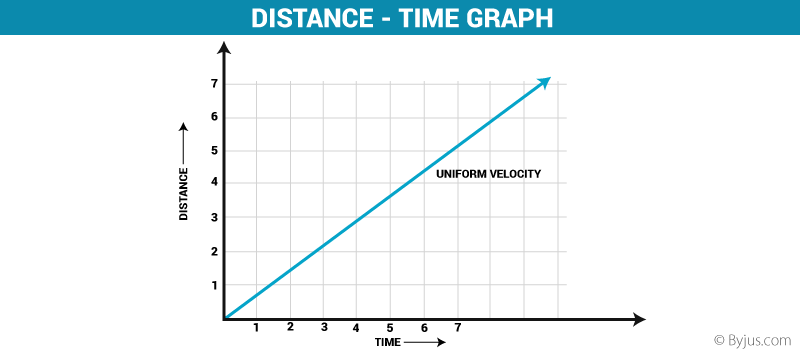
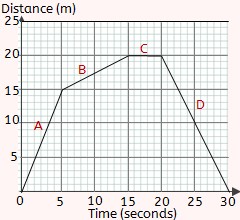
As we said, the slope equals the acceleration, a. time graph, we can also define one for a velocity vs. Just like we could define a linear equation for the motion in a position vs. For now, just remember that the area under the graph and the slope are the two important parts of the graph. We will do more with this information in a later chapter. This slope tells us that the car is not speeding up, or accelerating. Graphically, you can see that the slope of these two lines is 0. In our earlier example, we stated that the velocity was constant. The velocity curve also tells us whether the car is speeding up. The area under a velocity curve represents the displacement. This process is called dimensional analysis, and it is one of the best ways to check if your math makes sense in physics. For instance, if we end up with m × s for velocity instead of m/s, we know that something has gone wrong, and we need to check our math. This is good because it can tell us whether or not we have calculated everything with the correct units. You can treat units just like you treat numbers, so a km/km=1 (or, we say, it cancels out). If we add them together, we see that the net displacement for the whole trip is 0 km, which it should be because we started and ended at the same place. If we calculate the same for the return trip, we get –5 km. The units for minutes cancel each other, and we get 5 km, which is the displacement for the trip to school. Let’s take just the first half of the motion. In Figure 2.16, we have velocity on the y-axis and time along the x-axis. If we use a little algebra to re-arrange the equation, we see that d = v × × t. time graph to determine velocity, we can use a velocity vs. There are a few other interesting things to note. Second, if we have a straight-line position–time graph that is positively or negatively sloped, it will yield a horizontal velocity graph. First, we can derive a v versus t graph from a d versus t graph. This is important when dealing with circular motion.Figure 2.16 Graph of velocity versus time for the drive to and from school. Velocity, a vector quantity, changes if either the magnitude or the direction changes. It should also be noted that an object moving at a constant speed but changing direction continually is also accelerating. drawing a tangent to the curve at that timeĪs the diagram shows, after drawing the tangent, work out the change in distance (A) and the change in time (B).If an object is accelerating or decelerating, its speed can be calculated at any particular time by: The table shows what each section of the graph represents: Section of graph This can be shown as a curved line on a distance-time graph. If the speed of an object changes, it will be accelerating or decelerating. Distance-time graphs for accelerating objects - Higher The speed of an object can be calculated from the gradient of a distance-time graph.


 0 kommentar(er)
0 kommentar(er)
